Geum.ru

Содержание

Задачи оптимизации со многими неизвестными
Задача оптимизации туристических групп
1. Изучение функций ЕСЛИ, СЧЕТЕСЛИ. 2. Изучение фильтров.
Второй вариант
ABC-анализ с использованием фильтров

Подобный материал:

• Компьютерные (новые информационные) технологии обучения, 102.54kb.
• Название Предмет Направление, 921.62kb.
• «Информационные технологии в процессе обучения географии» Проблема над которой работает, 422.07kb.
• Пантелеев Владимир Иннокентьевич, к ф. м н., доцент кафедры математической информатики, 87.48kb.
• Информационные технологии как средство повышения эффективности обучения в школе, 63.19kb.
• Международная конференция «Информационные технологии в образовании и науке», 86.4kb.
• Программа собеседования по специальной профессиональной подготовке для абитуриентов,, 98.51kb.
• Г. И. Парамзина Новые информационные технологии обучения, 109.36kb.
• Программа «информатика и икт (информационные и коммуникационные технологии)», 443.93kb.
• Программа «информатика и икт (информационные и коммуникационные технологии)», 827.46kb.

Информационные технологии консультирования и обучения

магистратура «Управленческое консультирование в АПК»

Темы семинарских занятий

1. Групповая работа над документом Word. Рецензирование документа. Создание структурированного документа.
2. Разработка шаблона презентации для доклада (лекции), представления компании и нового бренда и т.д.
3. Excel. Задачи оптимизации. Задача оптимизации туристических групп. Выборочная обработка данных. Анализ данных с помощью фильтров.
4. Работа с поисковыми системами Интернет. Создание классификатора информационных ресурсов Интернет по видам информации, по различным критериям.
5. По материалам Интернета: поиск, обзор и классификация консалтинговых компаний России.
6. По материалам Интернета: поиск и обзор направлений управленческого консультирования.
7. По материалам Интернета: поиск и обзор подходов и мероприятий по антикризисному управлению.
8. По материалам Интернета: поиск и обзор систем моделирования и оптимизации бизнес-процессов предприятия.
9. По материалам Интернет: поиск и обзор методики управления предприятием с помощью Системы Сбалансированных Показателей (BSC).
10. По материалам Интернета: корпоративные системы, поиск, обзор, классификация. Основные функции и возможности.
11. Поиск, обзор и классификация систем электронной торговли, систем денежных расчетов, сиcтем Интернет-телефонии.
12. Поиск, обзор и классификация систем электронного документооборота.
13. По материалам Интернета: обзор подходов и стандартов управления проектами.
14. Подготовка иерархической структуры работ по проекту. Подготовка в MS Project перечня работ, назначение ресурсов, составление расписания.

Образец семинарского занятия №3. Excel. Задачи оптимизации

Задачи оптимизации со многими неизвестными

Для численного решения уравнений со многими неизвестными и ограничениями в Excel включен инструмент Поиск решения.

По умолчанию инструмент не установлен и его следует установить: вставьте дистрибутивный CD-диск и выберите в списке надстроек СервисНадстройки… соответствующий флажок.

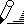
Если целевая функция и ограничения линейны, то решение состоит в нахождении множества чисел (х₁, х₂, … х_n), минимизирующих (максимизирующих) линейную целевую функцию f(х₁, х₂, … х_n)= c₁х₁+c₂х₂+… +c_nх_n при m =0 (где k=1, 2, … n). Инструмент Поиск решения обеспечивает максимум 200 изменяемых ячеек х_i при поиске решения (n_мах=200).

В качестве первого содержательного примера рассмотрим задачу о комбинезонах:

Ателье шьет комбинезоны трех типов К1, К2, К3 и использует ткани четырех типов Т1, Т2, Т3, Т4. Нормы расхода ткани каждого типа на каждый комбинезон и объем дневных затрат приведены на рис. ниже. Стоимость пошива

комбинезона типа К1 равна 100 руб., К2 – 120 руб., К3 – 110 руб. Дневной запас тканей в ателье следующий: ткани Т1 – 50м, ткани Т2 – 80м, ткани Т3 – 25м, ткани Т4 – 60м. Сколько комбинезонов каждого типа надо производить в день, чтобы получить максимальную стоимость производства? При этом использовать все типы тканей.

Переложим условие задачи на язык формул, т.е. опишем математическую оптимизируемую модель. В процессе решения надо найти дневной выпуск х₁, х₂ и х₃ каждого комбинезона, такой, чтобы получить максимум целевой функции 100х₁+120х₂+110х₃ при ограничениях

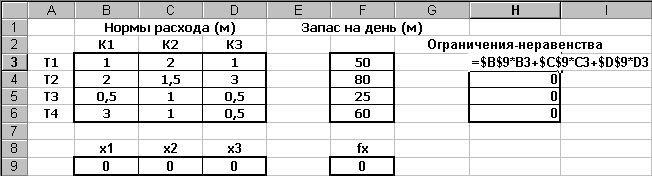
Теперь введем условие задачи в Excel, как показано ниже:

Как видно в ячейку Н3 введена формула =$B$9*B3+$C$9*C3+$D$9*D3, которая размножена на Н4:Н6. В ячейку F9 введена формула целевой функции =100*B9+120*C9+110*D9. В ячейках В9:D9 будет производиться подбор значения – здесь введены начальные значения х_i.

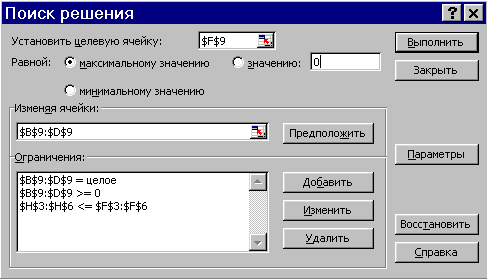
Далее вызываем инструмент СервисПоиск решения…, вводим адреса подготовленных ячеек и ограничения (как на рис. 2.39) и нажимаем кнопку Выполнить.

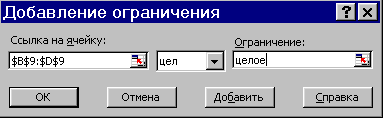
Заполнение окна Поиск решения не вызывает трудностей. Ограничения добавляются кнопкой Добавить; при этом появляется окно ввода ограничения:

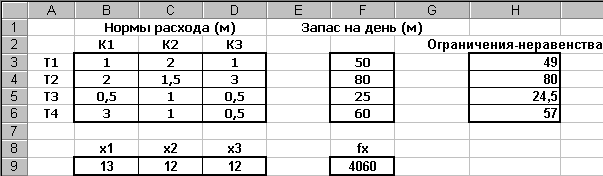
Результат вычислений показан на рис. 2.40:

Как видно, оптимальный дневной выпуск комбинезонов равен 13, 12 и 12. При этом в колонке Н видно, что часть тканей остается неизрасходованной.

Поэкспериментируйте: попробуйте вручную изменить подобранные значения (например, х1=14), оцените значения целевой функции и ячеек Н3:Н6. Повторно вызовите инструмент Поиск решения, удалите условие ($B$9:$D$9 = целое) и выполните подбор.

Обобщим проделанную работу и выделим этапы решения задачи оптимизации со многими неизвестными в Excel с помощью инструмента Поиск решения:

• анализ задачи, выделение свойств, параметров, ограничений;
• математическое описание оптимизируемой модели – введение обозначений, ограничений и создание целевой функции;
• грамотное размещение модели и поиск решения в Excel.

Задача оптимизации туристических групп

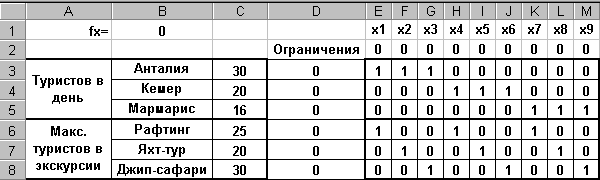
В качестве второго содержательного примера рассмотрим задачу формирования экскурсионных пакетов. Российская туристическая фирма ежедневно отправляет в три отеля Анталии, Кемера и Мармариса (Турция) соответственно 30, 20 и 16 человек. Экскурсионная программа каждой группы состоит из рафтинга (спуск по горной реке на плоту), яхт-тура вдоль побережья и путешествия джип-сафари в турецкую глубинку. Стоимость экскурсий с трансфером на человека для отелей разных городов следующая:

Рафтинг Яхт-тур Джип-сафари Анталия 55 20 35 Кемер 65 35 20 Мармарис 60 25 25

При этом существуют ограничения на количество человек в экскурсии: рафтинг – 25 чел., яхт-тур – 20 чел., джип-сафари – 30 чел. От каждого отеля на каждую экскурсию должно быть послано не менее 5 чел.

Необходимо определить оптимальное количество туристов для участия в каждой экскурсии при заданных ограничениях. Под оптимальностью понимать минимизацию суммарных расходов турфирмы.

Приступим к ее решению. Постановка задачи выполнена достаточно четко, поэтому можно сразу приступить к описанию математической модели. Введем обозначения подбираемых значений неизвестных х_i – число туристов каждого отеля на каждый вид экскурсии:

Рафтинг Яхт-тур Джип-сафари Анталия х₁ х₂ х₃ Кемер х₄ х₅ х₆ Мармарис х₇ х₈ х₉

Целевая функция (стоимость), которую следует минимизировать, запишется так:

Ограничения на ежедневное количество человек в экскурсиях:

Ограничения на ежедневное количество мест в экскурсиях:

Следующим шагом разместим оптимизируемую модель в Excel, как показано ниже:

Здесь, в ячейках Е2:М2 размещены начальные значения неизвестных (х₁, х₂, … х₉)=0. Для единообразной записи ограничений использована таблица коэффициентов Е3:М8. В ячейку D3 записана формула =E$2*E3+F$2*F3+G$2*G3+H$2*H3+I$2*I3+J$2*J3+K$2*K3+L$2*L3+M$2*M3, которая размножена на диапазон D4:D8. В ячейках С3:С8 записаны граничные значения числа туристов от отелей и в экскурсиях. Целевая функция записана в ячейке В1: =55*E2+20*F2+35*G2+65*H2+35*I2+20*J2+60*K2+25*L2+25*M2.

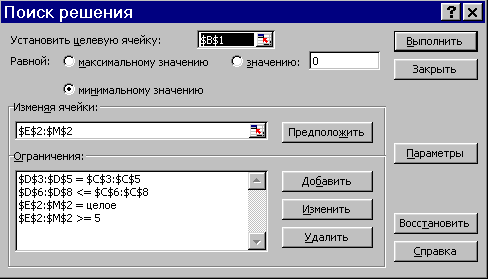
Нам осталось запустить поиск решения и ввести адреса ячеек и ограничения, как на рисунке ниже:

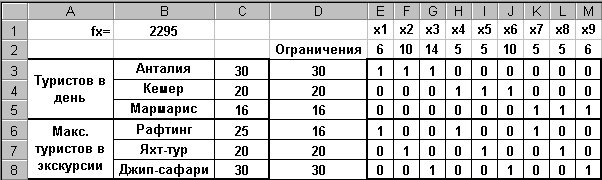
Результат поиска решения показан ниже:

Здесь в ячейках Е2:М2 подобрано оптимальное количество туристов, дающее минимальную стоимость расходов, равную 2295$. Проанализируйте полученное решение и поэкспериментируйте.

1. Изучение функций ЕСЛИ, СЧЕТЕСЛИ. 2. Изучение фильтров.

Функция ЕСЛИ, в зависимости от Условия, принимает Значение1 (если Условие верно) или Значение2 (если Условие не верно) и имеет следующий формат:

ЕСЛИ ( Условие ; Значение1_если_истина ; Значение2_если_ложь )

Выборочная обработка данных

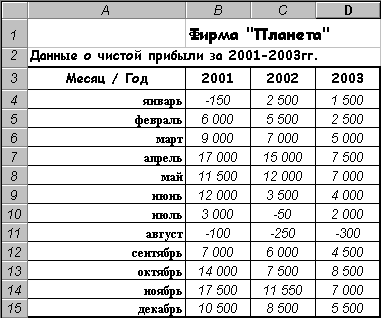
Задачи получения обобщенных данных, выборочной обработки данных по некоторым критериям могут решаться в Excel различными способами. Рассмотрим задачу получения обобщенных данных из таблицы (рис. 2.29) прибылей фирмы за три года по месяцам. По каждому году требуется определить количество убыточных месяцев, сумму убытков, максимальную прибыль за месяц и среднемесячную прибыль.

Первый, самый простой вариант решения может выглядеть так:

Воссоздайте это решение — в ячейках B18:B21 записаны следующие формулы:

в В18 – =СЧЁТЕСЛИ(B4:B15;»

Мой швейный путь. Почему я не люблю конструирование.

15 лет назад я получила диплом по профессии Портной-закройщик. С этого момента началась моя профессиональная деятельность. Но начала я шить гораздо раньше.

В 7 классе у нас начались уроки труда, нас посадили за швейные машинки. Шили фартуки, юбочки еще что-то, я уже не помню. Но помню что в старших классах (9-11) шила себе одежду: маечки, шортики, юбочки. Без выкроек! Перерисовывала сразу на ткани с готовых вещей. И все получалось и носилось! Шила на машинке с ручным приводом

Во время учебы на портного, а училась я по Единой методике конструирования легкой женской одежды, нам дали базовые знания по конструированию и моделированию.
Так вот, когда мы строили, например, базовую выкройку платья (именно с построения базы или выкройки-основы начинается любая выкройка), нам давали при построении прибавку на свободу 5 см! Мы строили, кроили и этот балахон примеряли. И у меня в мыслях не было, что преподаватель плохой, что он не правильно дает нам информацию. Я хотела выкройку по фигуре, а получила балахон.
Этот балахон на примерке мы садили на свою фигуру и в итоге получали что хотели, но каким трудом)))! И так каждое изделие!

Когда я шила без выкроек и у меня было все хорошо, я шила без проблем. А когда я получила профессиональные знания по конструированию, я шить не смогла, мне казалось это сложно, нудно. Строишь, вычисляешь, а получается чушь, которую нужно подгонять и подгонять.. Я была разочарована. И лет 5-6 после учебы я не могла себе ни чего сшить.

После учебы я работала 6 лет на разных швейных фабриках, на массовке. Думала, там то меня научат. Меня научили шить быстро и по прямой, и конечно качественно, ни один технолог не пропустит твой косяк в продажу. По началу целыми днями «порола». Но за год работы привыкаешь, врабатываешься и понимаешь, что массовка это скучно и ни чему не учит. Было так скучно, что я параллельно училась и получила еще почти два образования(не связанных с шитьем).

И вот однажды, мне понадобилось платье, которое я ни как не могла найти в магазинах. То цвет не нравится, то длина. Вообщем, психанула и сшила платье сама, по своей фигуре, нужного мне цвета!

И решила я бросить массовку и пойти учиться дальше шитью, но профессионального образования нужного уровня у нас в городе нет. Поэтому я пошла другим путем, училась напрямую у профессионалов. В ателье, общалась с конструкторами по возможности, и шила, шила, шила. Тренировалась без остановки, пока не поняла для себя всю философию этого мира!

В ателье.. Выкройками и кроем занималась конструктор-модельер с инженерным образованием. Для меня просто «БОГ» выкроек. Так вот иногда, изделие, чтоб оно село так как нужно на клиента приходилось примерять по 5 раз(это по выкройке, которую сделал БОГ). И клиенты приходили на 5 примерок, потому что хотели получить идеал!
И у меня в мыслях не было, что это плохой конструктор, потому что в итоге клиент уходил довольный.

Поэтому я не люблю конструирование!? Считаешь, думаешь, чертишь, стараешься, для каждого изделия своя выкройка. Для каждого индивидуального человека свои расчеты, своя прибавка на свободу, которую узнаешь только в ходе примерок. То есть все равно приходится на примерке доводить до идеала. Мне проще сразу перейти от готовой выкройки к примерке! И на примерке уже посадить, так как нужно.

Я работаю с готовыми выкройками уже 6 лет, ни одна выкройка с которой я работала не была плохой. Наоборот я вздохнула с облегчением, наконец-то мне не нужны формулы, расчеты, построения одних и тех же четких линий. Я подобрала для себя готовые выкройки, которые мне больше всего подходят и в работе с которыми меньше возникает проблем и больше не мучаюсь с конструированием базы))
Подробнее о том, что такое готовая выкройка для меня, рассказала в этой статье

Готовые выкройки верхней одежды тут
Готовая выкройка для платьев тут

У меня есть парочка детских журналов Оттобре. Из этих журналов я беру выкройки толстовок, брюк и все что мне нужно. По детским журналам шью себе и мужу, так как 170 рост по журналу соответсвует 44-46 размеру одежды, как раз на нас с мужем))

Мне нравятся готовые конструктивные решения из журналов Бурда, ими тоже пользуюсь при необходимости.

И вместо выводов:

Да, когда за плечами 15 лет опыта, легко шить и легко творить что хочется! То, чему учили в начале пути, я благополучно забыла, мне больше это не нужно, все полученные знания я отработала на практике! Я конечно продолжаю учиться, потому что профессия у нас такая, все знать и охватить жизни не хватит. Каждое новое изделие это обучение чему то новому.. новый узел, новая ткань, новая форма..

А главное Шитье для меня это творчество!

А в творчестве МОЖНО ВСЕ! ЗАПРЕТОВ НЕТ! НЕТ ГРАНИЦ И ЖЕСТКИХ ПРАВИЛ!

Главный критерий- ТВОРИТЬ С УДОВОЛЬСТВИЕМ!

Чего и вам желаю: творить с удовольствием! Получать радость от созидания!

НО АЗЫ любого направления полезно знать для минимизации своих усилий и во избежание изобретения «велосипеда».

Подписывайтесь, ставьте лайки! Мне будет приятно)

ПыСы: Не вижу смысла спорить ни с кем, у каждого свой путь! И уж тем более не вижу смысла в негативных комментариях)) Люди будьте уже наконец счастливы. И делитесь счастьем. Ваш негатив, он только ваш, больше он ни кому не нужен.
Всем добра.