Выкройка для бейсбольного мяча

Здравствуйте, TheReader, Вы писали:

Я признал выше, что накосячил — в том смысле, что угол на самом деле посчитал неверно.
Заметьте, мы исходим из того предположения, что размеры на исходной выкройке указаны правильно (иначе нехрен это вообще обсуждать )).
Я сначала сделал вольное допущение о равенстве дуг и посчитал угол исходя из этого.
Но ТС указал на ошибку, и исходные размеры тупо показывают, что из банальнйо теоремы Пифагора радиус соединяющей дуги R=15,5 и тогда (опять тупо — тангенс известен) угол aplha=18.9 градуса.

TR>BC должно быть равно BD:

Сори, не соглашусь. Смысл физический в этом какой? DB — это дуга которая внутри детали, к ней ничего не примыкает.
Вот рисунок, с учетом ваших обозначений, я на нем попытался криво-косо заодно изобразить еще и свернутую деталь:

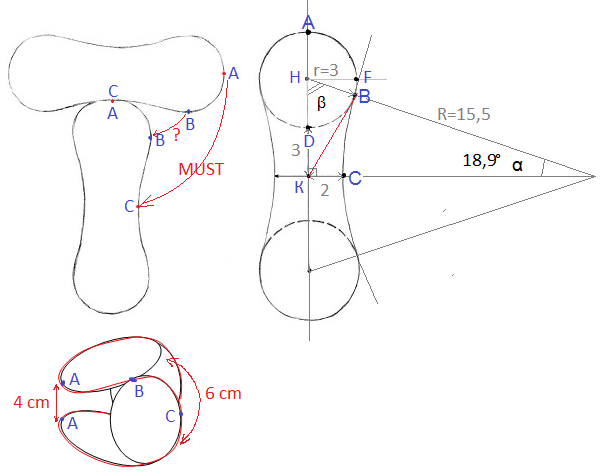
TR>Для этого проводим перпендикуляр к AD через центр окружности. И ставим т.F справа на пересечении перпендикуляра и самой окружности.

Посмотрите на рисунок: «окружности» выкройки, сворачиваяь, ложатся не параллельно друг ддругу (ну банально с одной стороны между ними 6 см, а с другой — 4). Поэтому «ответные окружности» второй детали касаются «первых» окружностей не в точке F, а где-то как раз около точки B (что меня и толкнуло предположить, что AB=BC — посмотрите на левую схемку, там мое предположение, что В одной детали соединяется с В другой — что вовсе не обязательно.

TR>Далее понимаем, что AF должно быть равно CF и равно DF.

не понял почему «AF должно быть равно CF».

TR>Из этого следует, что DB=AF-BF и CB=CF-BF=AF-BF.
TR>Следовательно DB=BC

и вывод имхо неправильный, и непонятно какой физичсекий смысл.

TR>Но так решить задачу можно, но сложно.
TR>проще:
TR>ставим точки:
TR>K в центре рисунка(между цифрами 3 и 2)
TR>H в центре верхней окружности.
TR>проводим KB (перпендикуляр к BH)

почему вы решили что это перпендикуляр? Тогда КВ — касательная к обеим окружнсотям? Отчего она обязана ею быть?

TR>по теореме синусов
TR>KH/sin(KBH)=BH/sin(HKB)
TR>KH=2*3.14*BH

TR>(2*3.14*BH)/sin(KBH)=BH/sin(HKB)
TR>sin(KBH)=1, т.к. это угол 90градусов

почему он 90 градусов? откуда следует?

TR>(2*3.14*BH)=BH/sin(HKB)
TR>(2*3.14*BH)/BH=1/sin(HKB)
TR>BH/(2*3.14*BH)=sin(HKB)
TR>HKB=arcsin(BH/(2*3.14*BH))

TR>угол KHB=90-HKB

TR>Дальше все совсем просто. если нужно, допишу, если будут требования зрителей.

поясните плиз, какой именно факт вы хотели доказать.

	От:	TheReader
	Дата:	17.11.10 12:16
Оценка:

Здравствуйте, Skelterer, Вы писали:

S>Я признал выше, что накосячил — в том смысле, что угол на самом деле посчитал неверно.
S>Заметьте, мы исходим из того предположения, что размеры на исходной выкройке указаны правильно (иначе нехрен это вообще обсуждать )).

S>Я сначала сделал вольное допущение о равенстве дуг и посчитал угол исходя из этого.
S>Но ТС указал на ошибку, и исходные размеры тупо показывают, что из банальнйо теоремы Пифагора радиус соединяющей дуги R=15,5 и тогда (опять тупо — тангенс известен) угол aplha=18.9 градуса.

TR>>BC должно быть равно BD:

S>Сори, не соглашусь. Смысл физический в этом какой? DB — это дуга которая внутри детали, к ней ничего не примыкает.
S>Вот рисунок, с учетом ваших обозначений, я на нем попытался криво-косо заодно изобразить еще и свернутую деталь:

TR>>Для этого проводим перпендикуляр к AD через центр окружности. И ставим т.F справа на пересечении перпендикуляра и самой окружности.

S>Посмотрите на рисунок: «окружности» выкройки, сворачиваяь, ложатся не параллельно друг ддругу (ну банально с одной стороны между ними 6 см, а с другой — 4). Поэтому «ответные окружности» второй детали касаются «первых» окружностей не в точке F, а где-то как раз около точки B (что меня и толкнуло предположить, что AB=BC — посмотрите на левую схемку, там мое предположение, что В одной детали соединяется с В другой — что вовсе не обязательно.

TR>>Далее понимаем, что AF должно быть равно CF и равно DF.

S>не понял почему «AF должно быть равно CF».

TR>>Из этого следует, что DB=AF-BF и CB=CF-BF=AF-BF.
TR>>Следовательно DB=BC

S>и вывод имхо неправильный, и непонятно какой физичсекий смысл.

Полностью с Вами согласен. Я был неправ в утверждениях выше.

TR>>Но так решить задачу можно, но сложно.
TR>>проще:
TR>>ставим точки:
TR>>K в центре рисунка(между цифрами 3 и 2)
TR>>H в центре верхней окружности.
TR>>проводим KB (перпендикуляр к BH)

S>почему вы решили что это перпендикуляр? Тогда КВ — касательная к обеим окружнсотям? Отчего она обязана ею быть?

1) Проводим перпендикуляр к BH через точку K.
2) KB- касательная к обеим окружностям.

TR>>по теореме синусов
TR>>KH/sin(KBH)=BH/sin(HKB)
TR>>KH=2*3.14*BH

TR>>(2*3.14*BH)/sin(KBH)=BH/sin(HKB)
TR>>sin(KBH)=1, т.к. это угол 90градусов

S>почему он 90 градусов? откуда следует?

Потому, что мы провели перпендикуляр к BH через точку K. (см выше)

TR>>(2*3.14*BH)=BH/sin(HKB)
TR>>(2*3.14*BH)/BH=1/sin(HKB)
TR>>BH/(2*3.14*BH)=sin(HKB)
TR>>HKB=arcsin(BH/(2*3.14*BH))

TR>>угол KHB=90-HKB

TR>>Дальше все совсем просто. если нужно, допишу, если будут требования зрителей.

S>поясните плиз, какой именно факт вы хотели доказать.

то, что можно вычислить угол beta.
после того, как известен угол beta, можно посчитать размеры и остальные углы треугольника KH[крайняя правая точка]
после этого можно вычислить KC, а после KC — расстояние между центрами.
когда мы знаем эти цифры — знаем длину окружности мяча, а следовательно, и диаметр.

Немного не с той стороны, но так проще.

Задача ведь сводилась к тому, как вывести зависимость R от диаметра мяча ? Или я неверно все понял ?

	От:	Skelterer
	Дата:	17.11.10 13:55
Оценка:

Здравствуйте, TheReader, Вы писали:

S>>

TR>Задача ведь сводилась к тому, как вывести зависимость R от диаметра мяча ? Или я неверно все понял ?

R в исходных размерах вычиляется тривиально, далее тривиальное скалирование по пропорции: в заданных размерах диаметр мяча = 7см, ну значит надо все умножить на ( /7). То есть это не задача для такого усиленного обсуждения )).

Лично я пытался сообразить две вещи:
1) действительно ли обсуждаемая кривая с радиусом R является дугой окружности?
2) почему выбраны именно такие размеры, а не другие? Оригинальные размеры KD=3 и КС=2 задают «перекос» двух круглых деталей относительно друг друга, а вместе с радиусом r они задают и диаметр результирующего мячика. В частности выбраны такие размеры, что AB != BC, и это странно, потому что точка В — точка перегиба (изменение направления кривизны), и в идеале хотелось бы, чтобы эта точка самосовмещалась при соединениюю с ответнйо деталью.

TR>1) Проводим перпендикуляр к BH через точку K.
TR>2) KB- касательная к обеим окружностям.
TR>Потому, что мы провели перпендикуляр к BH через точку K. (см выше)

сори. Вы просто волюнтаристски соединили точки К и В )). А если «провели через К перпендикуляр», то откуда следует, что перпендикуляр из точки K к прямой ВН пересекает эту прямую именно в В?

S>>поясните плиз, какой именно факт вы хотели доказать.
TR>то, что можно вычислить угол beta.

он вычисляется сразу после того, как стал известен R. Это тупо арктангенс((R+2)/(r+3)). Где 3=KD, 2=KC — заданные размеры. То есть beta=71гр.

	От:	TheReader
	Дата:	17.11.10 16:27
Оценка:

Здравствуйте, Skelterer, Вы писали:

S>Здравствуйте, TheReader, Вы писали:

S>>>

TR>>Задача ведь сводилась к тому, как вывести зависимость R от диаметра мяча ? Или я неверно все понял ?

S>R в исходных размерах вычиляется тривиально, далее тривиальное скалирование по пропорции: в заданных размерах диаметр мяча = 7см, ну значит надо все умножить на ( /7). То есть это не задача для такого усиленного обсуждения )).

S>Лично я пытался сообразить две вещи:
S>1) действительно ли обсуждаемая кривая с радиусом R является дугой окружности?
S>2) почему выбраны именно такие размеры, а не другие? Оригинальные размеры KD=3 и КС=2 задают «перекос» двух круглых деталей относительно друг друга, а вместе с радиусом r они задают и диаметр результирующего мячика. В частности выбраны такие размеры, что AB != BC, и это странно, потому что точка В — точка перегиба (изменение направления кривизны), и в идеале хотелось бы, чтобы эта точка самосовмещалась при соединениюю с ответнйо деталью.

TR>>1) Проводим перпендикуляр к BH через точку K.
TR>>2) KB- касательная к обеим окружностям.
TR>>Потому, что мы провели перпендикуляр к BH через точку K. (см выше)

S>сори. Вы просто волюнтаристски соединили точки К и В )). А если «провели через К перпендикуляр», то откуда следует, что перпендикуляр из точки K к прямой ВН пересекает эту прямую именно в В?

B находится на окружности. B находится и на второй окружности. если принять, что обе окружности должны плавно переходить одна в другую и В — точка смены кривизны, то радиусы, проведенные из центров окружностей к т.В будут образовывать прямую.
то есть BH не сама по себе, а часть B[неизвесная буква-центр радиуса R]

S>>>поясните плиз, какой именно факт вы хотели доказать.
TR>>то, что можно вычислить угол beta.

S>он вычисляется сразу после того, как стал известен R. Это тупо арктангенс((R+2)/(r+3)). Где 3=KD, 2=KC — заданные размеры. То есть beta=71гр.

а откуда Вы узнаете R ? кроме как померять линейкой ? А если мерять линейкой, то проще поэкспериментировать с вырезками из бумаги — типа макеты

То есть я хочу сказать, что приблизительно Вы сможете и без математики сделать, а если с математикой — то линейка тут только мешает.
И 3=KD, 2=KC (заданные размеры) при правильном расчете не исходные данные, а вычисляемые в зависимости от диаметра мяча.

Меня заинтересовала данная задачка именно с математической точки зрения, т.к. делать мяч я не собираюсь

Шьем лоскутные мячики

Этот мастер-класс я, в первую очередь, адресую мамам малышей и педагогам, занимающимися с маленькими детьми. Также я постаралась сделать максимально детальное описание процесса, чтобы мячик могли сшить дети или взрослые, которые берут в руки иголку с ниткой не так часто и уж тем более, не знакомы с лоскутной техникой.

На создание мастер-класса меня вдохновила прекрасная книга Галины Дайн «Лоскутные мячики», но как построить выкройку для шестиклинного мячика, я так и не разобралась. Пришлось действовать методом подбора. После пары неудачных попыток я все-таки пришла к устроившему меня результату. Моя годовалая с небольшим дочка тоже была очень довольна результатом. Она полюбила играть в мячики, бросает их, катает, разглядывает. Мячики можно стирать в машине, что немаловажно. Я приготовила для мастер-класса два мячика, один сшила вручную, другой на машинке. Хочу поделиться процессом изготовления.

Диаметр — около 8 см, что чуть больше теннисного арабского мячика.

Из материалов понадобятся плотная ткань типа бязи или хлопка для пэчворка, наполнитель холлофайбер «шарики», контейнер из-под бахилл, несколько бусин, нитки.

Вообще-то, ткань может подойти практически любая, я использовала и плащевку, и флис, получалось хорошо. Главное, чтобы материал держал форму, не сильно тянулся. Вместо холлофайбера «шарики» можно использовать распотрошенный синтепон или ватин, можно мелко порезать капроновые колготки. Но именно «шарики» лучше всего подходят для набивки, к тому же этот материал гипоаллергенен.

Контейнеры из-под бахилл обычно накапливаются в карманах после посещения медицинских учереждений, но можно купить готовую «гремелку» для мягких игрушек или сделать самим из двух крышечек от пластиковых бутылок. Для этого надо взять две крышки, положить в одну несколько бусин, накрыть второй и плотно обмотать скотчем.

Определитесь с тканью. Можно сделать мячик однотонный, можно из двух, трех цветов или из шести.

Возьмите обычный тетрадный лист в клеточку и начертите выкройку клинышка для мячика по схеме. По клеточкам это легко сделать.

На ткани клинышек надо положить «наискосок», нить основы, то есть долевая, должна проходить, как показано на выкройке. Это очень важно. Даже если вы выбрали трикотаж, располагайте клинышек под углом 45 градусов по отношению к кромке ткани.

Запас на шов делаем 0,5-0,7 см. Обведите выкройку и вырежете деталь с учетом запаса на шов. Я обводила обычным простым карандашом. Если ваш мячик будет двухцветный, то три детали надо выкроить их одной ткани, три — из другой. Если трехцветный, то по две детали из каждой ткани и т.д.

Далее — два способа шитья.

Вариант 1. Шьем вручную.

Этот мячик я сделала из трех различных по рисунку и цвету тканей.

Выкраиваем клинышки и сразу раскладываем их на столе по очередности, как они будут располагаться в готовом мячике.

Берем две крайние слева детали и сшиваем их швом «назад иголкой» от одной вершины детали до другой.

Присоединяем таким же способом следующую деталь.

И следующую, пока не будут сшиты между собой все шесть клиньв. Оставьте незашитым отверстие для выворачивания и набивки, это половинка одной из сторон, как показано на фото ниже.

Теперь заготовку мячика можно вывернуть на лицевую сторону.

Набиваем наш мячик до половины.

Затем вложите внутрь «гремелку» — у меня это контейнер из-под бахилл с бусинами — и набейте мячик полностью. Причем часть набивки должна выглядывать из отверстия, как бы вываливаться. Мы потом заправим ее в процессе зашивания отверстия.

Теперь подверните внутрь припуски на шов вдоль сторон отверстия и, сжав мячик рукой, чтобы края отверстия сошлись вместе, зашейте его потайным швом, заправляя набивку внутрь.

Соедините в одну точку клинышки на вершине мячика, если они разошлись.

Вариант 2. Сшиваем детали на швейной машинке.

Этот мячик я сделала двухцветным, выкроила три детали из желтой ткани, три — из голубой и разложила их на столе в две кучки: желтый-голубой-желтый и голубой-желтый-голубой. Сделала только одну фотографию, вторую забыла.

Сколола булавками и стачала два клинышка разных цветов. Когда я делала другой мячик, из флиса и льна, детали сначала сметывала. Не поленитесь, сметайте, если работаете с трикотажем или редко садитесь за машинку. Так получится аккуратнее. Стачиваем детали, как на фото ниже: от края среза до края. На концах швов делаем закрепки, 2-3 стежка.

Подкалываем еще один клинышек и стачиваем. Припуск — в разутюжку.

После того, как у нас получилась заготовка из трех клиньев, откладываем ее в сторону и аналогичным образок делаем вторую заготовку. У нас готовы две половинки мячика.

Выворачиваем на лицевую сторону одну из половинок.

Вкладываем одну половинку в другую, скалываем булавками или сметываем, аккуратно совмещая вершины половинок.

Стачиваем две половинки мячика, оставляя незашитым участок на одной из сторон.

Мячик выворачиваем. Если сделали все аккуратно, то получается ровная вершина.

Затем подгибаем внутрь запасы на шов и зашиваем отверстие потайным швом, сжимая мячик в руке, чтобы сошлись края отверстия.

Можно мячики декорировать, пришивая вручную сверху на швы шнур или узкую ленту. Если вершины мяча получились не очень аккуратными, их можно спрятать, если нашить красивые пуговицы. Я на некоторые из мячиков нашила обтянутые тканью плоские пуговицы. Чтобы сделать такую пуговицу, возьмите пуговицу без ножки (можно вместо пуговицы вырезать кружок из пластиковой бутылки размером с монету 50 копеек), положите пуговицу на ткань, обведите и вырежьте кружок с запасом на шов, равным радиусу пуговицы. Соберите кружок ткани по краю на сборку, вложите внутрь пуговицу, затяните нитку и закрепите.

Надеюсь, что мой мастер-класс окажется полезен, особенно начинающим в шитье.